Công thức đạo hàm logarit
➤ Định nghĩa ngắn gọn:
Đạo hàm của hàm logarit cho biết tốc độ thay đổi của hàm số logarit theo biến đầu vào. Dưới đây là các công thức quan trọng bạn cần nhớ:
✅ a) Đạo hàm của logarit tự nhiên:
Hàm: y=ln(x)
Công thức: (dy/dx)=1 / x
Điều kiện: x > 0
✅ b) Đạo hàm của logarit cơ số a:
Hàm: y=logₐ(x)
Công thức: (dy/dx)=1 / [x * ln(a)]
Điều kiện: x > 0, a > 0, a ≠ 1
✅ c) Đạo hàm của logarit hàm hợp:
Nếu y=ln(u(x)) → dy/dx=u' (x) / u(x)
Nếu y=logₐ(u(x)) → dy/dx=u' (x) / [u(x) * ln(a)]
🎯 Ví dụ minh họa:
Cho y=ln(3x + 1)
⇒ dy/dx=3 / (3x + 1)

Đạo hàm logarit là gì? Tổng hợp công thức đạo hàm của logaritĐạo hàm logarit không chỉ dùng trong các bài toán " rõ ràng là logarit" , mà còn rất hiệu quả trong các biểu thức phức tạp. Dưới đây là 6 tình huống tiêu biểu nên áp dụng:
Hàm số đã có dạng logarit từ đầu
Ví dụ: y=ln(x), y=logₐ(u(x)), ...
→ Áp dụng công thức cơ bản trực tiếp.
Hàm là tích, thương hoặc lũy thừa phức tạp
→ Dùng logarit hóa để biến đổi thành tổng hiệu logarit → đạo hàm dễ hơn.
📌 Ví dụ:
y=[(x² + 1)^5 * √ (x + 3)] / (x - 1)^3
→ ln(y)=5ln(x² + 1)+0.5ln(x + 3) - 3ln(x - 1)
→ Đạo hàm 2 vế dễ dàng.
Hàm hợp chứa logarit
→ Dùng quy tắc hàm hợp kết hợp đạo hàm logarit.
Ví dụ: y=ln(2x² + 1) → y' =(4x) / (2x² + 1)
Các bài toán khảo sát, tìm cực trị
Ví dụ: y=xln(x) → y' =ln(x)+1 → giải y' =0 để tìm cực trị.
Bài toán mô hình thực tế
Trong các tình huống về tài chính, vật lý, sinh học, … logarit xuất hiện tự nhiên.
Ví dụ: A=Pe^(rt) → giải t bằng logarit
Hoặc pH=-log[H⁺] → đạo hàm logarit để tìm tốc độ thay đổi pH
Rút gọn biểu thức đạo hàm khó trước khi tính giới hạn
→ Đạo hàm logarit giúp tối giản biểu thức, giảm sai sót khi giải.
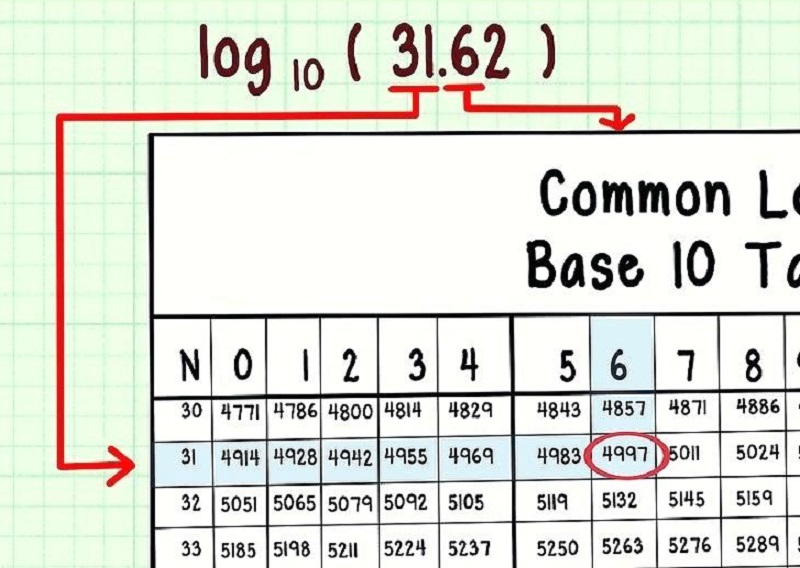
Khi nào nên áp dụng đạo hàm logarit?✅ a) Nhớ công thức gốc:
(d/dx)[ln(x)]=1 / x
✅ b) Nhớ quy tắc hàm hợp:
y=ln(u(x)) → y' =u' (x) / u(x)
👉 Mẹo: “ Đạo hàm tử – giữ nguyên mẫu”
✅ c) Nhớ công thức có logₐ:
(d/dx)[logₐ(x)]=1 / [x * ln(a)]
→ Luôn chia thêm ln(a) ở mẫu nếu cơ số ≠ e
✅ d) So sánh dễ nhớ:
Biểu thức
Đạo hàm
ln(x)
1 / x
ln(u(x))
u' (x) / u(x)
logₐ(x)
1 / (x * ln(a))
logₐ(u(x))
u' (x) / [u(x) * ln(a)]
✅ e) Luyện tập bằng ví dụ đơn giản
Ví dụ:
y=ln(2x) → y' =2 / (2x)=1 / x
y=log₂(x³ + 1) → y' =3x²/ [(x³ + 1) * ln(2)]
✅ f) Ghi nhớ qua ứng dụng:
Sử dụng flashcard (Quizlet, Anki), viết lại công thức nhiều lần, luyện đề thật giúp nhớ lâu, hiểu sâu.

Mẹo ghi nhớ công thức đạo hàm logarit nhanh và chính xác📘 DẠNG 1: Tính đạo hàm hàm logarit cơ bản
Ví dụ 1:
Tính đạo hàm của: y=ln(x)
Lời giải:
y' =1 / x (điều kiện: x > 0)
Ví dụ 2:
Tính đạo hàm của: y=log₃(x)
Lời giải:
y' =1 / (x · ln(3)) (điều kiện: x > 0)
📘 DẠNG 2: Đạo hàm hàm hợp có chứa logarit
Ví dụ 1:
Cho y=ln(2x + 1). Tính y' .
Lời giải:
y' =2 / (2x + 1)
Ví dụ 2:
Tính đạo hàm của: y=log₂(x² + 1)
Lời giải:
y' =(2x) / [(x² + 1) · ln(2)]
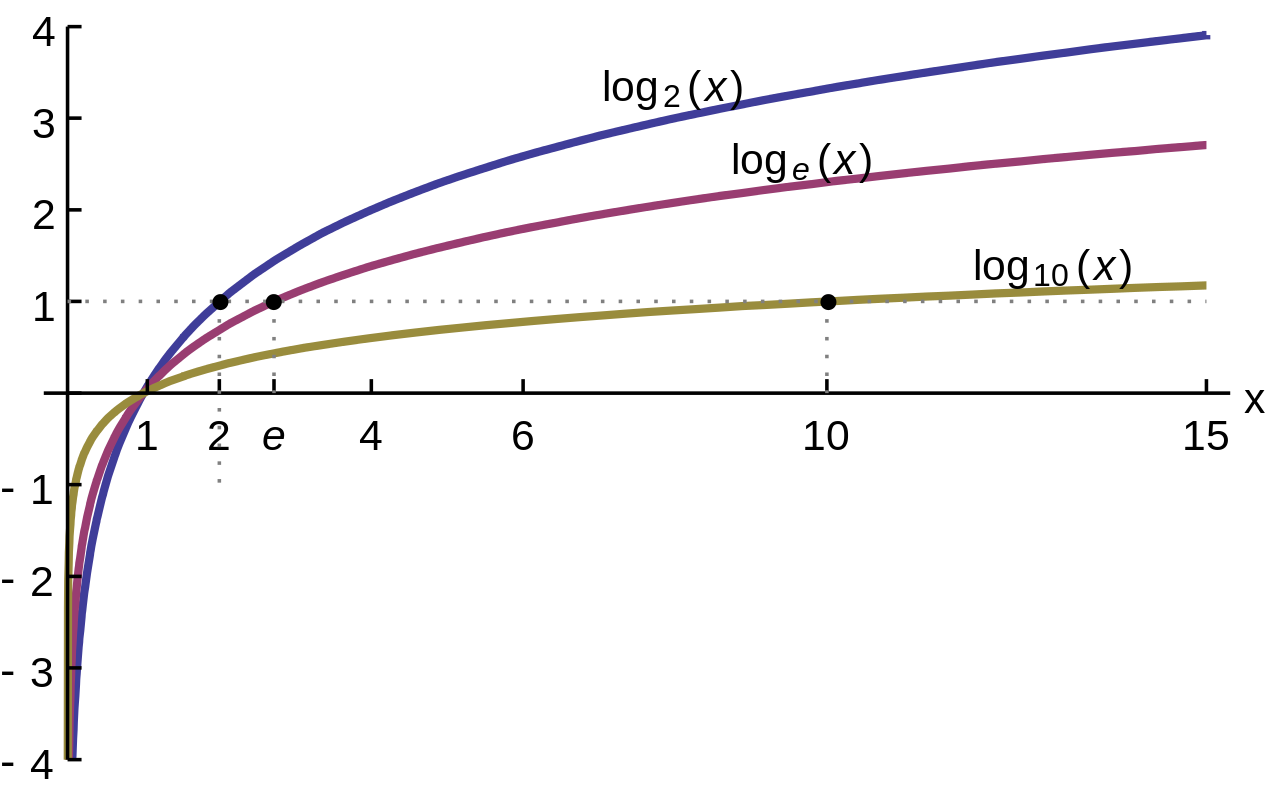
Các dạng bài tập đạo hàm logarit có lời giải phổ biến📘 DẠNG 3: Đạo hàm biểu thức phức tạp bằng logarit hóa
Ví dụ:
Cho y=[(x² + 1)³ · √ (x + 1)] / (x³ - 2)² . Tính y' .
Bước 1: Lấy logarit 2 vế:
ln(y)=3ln(x² + 1)+½ ln(x + 1) – 2ln(x³ – 2)
Bước 2: Đạo hàm 2 vế:
(y' /y)=(6x)/(x² + 1)+1/[2(x + 1)] – (6x² )/(x³ – 2)
Bước 3: Nhân 2 vế với y:
y' =y · [(6x)/(x² + 1)+1/[2(x + 1)] – (6x² )/(x³ – 2)]
📘 DẠNG 4: Khảo sát hàm số chứa logarit
Ví dụ:
Xét chiều biến thiên của hàm số: y=x · ln(x)
Lời giải:
y' =ln(x)+1
Giải phương trình y' =0:
ln(x)+1=0 → x=1/e
Kết luận:
Hàm nghịch biến trên (0; 1/e)
Hàm đồng biến trên (1/e; +∞ )
📘 DẠNG 5: Bài toán thực tế có logarit
Ví dụ:
Lượng chất phóng xạ giảm theo: N(t)=N₀ · e^(– kt)
Tính tốc độ phân rã tại t=5
Lời giải:
N' (t)=– k · N₀ · e^(– kt)
⇒ N' (5)=– k · N₀ · e^(– 5k)
📘 DẠNG 6: Tính giới hạn có chứa logarit
Ví dụ:
Tính: limₓ→ 0⁺ [ln(1 + x)/x]
Lời giải:
limₓ→ 0⁺ [ln(1 + x)/x]=1
(Đây là giới hạn cơ bản thường dùng)
✅ Gợi ý cách học hiệu quả:
- Hiểu bản chất của đạo hàm logarit trước khi học thuộc lòng công thức. Nắm được lý do vì sao công thức có dạng như vậy sẽ giúp bạn ghi nhớ sâu và lâu hơn.
- Ghi nhớ công thức bằng các mẹo học ngắn gọn, dễ nhớ, chẳng hạn như “ đạo hàm tử – giữ mẫu” cho hàm hợp ln(u(x)), hoặc nhớ rằng logarit thì “ chia ln(a)” còn mũ thì “ nhân ln(a)” .
- Tự tạo một bảng tổng hợp các công thức đạo hàm của logarit cơ bản và hàm hợp. Việc hệ thống kiến thức theo bảng giúp dễ học, dễ tra cứu và tăng khả năng ghi nhớ.
- Thường xuyên luyện tập với các ví dụ đa dạng, từ cơ bản đến nâng cao. Làm bài theo từng dạng giúp bạn nhận diện nhanh được phương pháp giải phù hợp.
- Tập trung ôn luyện theo chuyên đề như: đạo hàm hàm hợp, đạo hàm biểu thức phức tạp bằng logarit hóa, khảo sát hàm có chứa logarit, … giúp bạn hiểu sâu từng phần.
- Chủ động giải lại những bài tập từng làm sai để rút kinh nghiệm, tránh lặp lại lỗi tương tự trong đề thi thật.
- Cố gắng liên hệ các công thức đạo hàm của logarit với các ứng dụng thực tế trong đời sống (tài chính, sinh học, vật lý… ) để việc học trở nên thú vị và dễ nhớ hơn.
Việc hiểu và vận dụng đúng công thức đạo hàm logarit sẽ giúp bạn tiết kiệm thời gian làm bài, xử lý tốt các bài toán phức tạp và đạt điểm cao trong các kỳ thi. Đừng chỉ học thuộc – hãy luyện tập thường xuyên và áp dụng linh hoạt để ghi nhớ lâu và hiểu sâu bản chất. Đây chính là chìa khóa để bạn chinh phục mọi dạng bài liên quan đến logarit một cách tự tin và hiệu quả.