Công thức đạo hàm logarit
Đạo hàm của hàm logarit là quy tắc dùng để tính tốc độ thay đổi của hàm logarit theo biến số.
Đạo hàm của logarit tự nhiên (cơ số e):
Công thức:
(d/dx)[ln(x)]=1 / x
Điều kiện: x > 0
Đạo hàm của logarit cơ số a (với a > 0, a ≠ 1):
Công thức:
(d/dx)[logₐ(x)]=1 / (x * ln(a))
Điều kiện: x > 0
Đạo hàm của logarit hàm hợp:
Nếu y=ln(u(x)) thì:
dy/dx=u' (x) / u(x)
Nếu y=logₐ(u(x)) thì:
dy/dx=u' (x) / [u(x) * ln(a)]
Ví dụ:
Cho y=ln(3x + 1)
⇒ dy/dx=3 / (3x + 1)
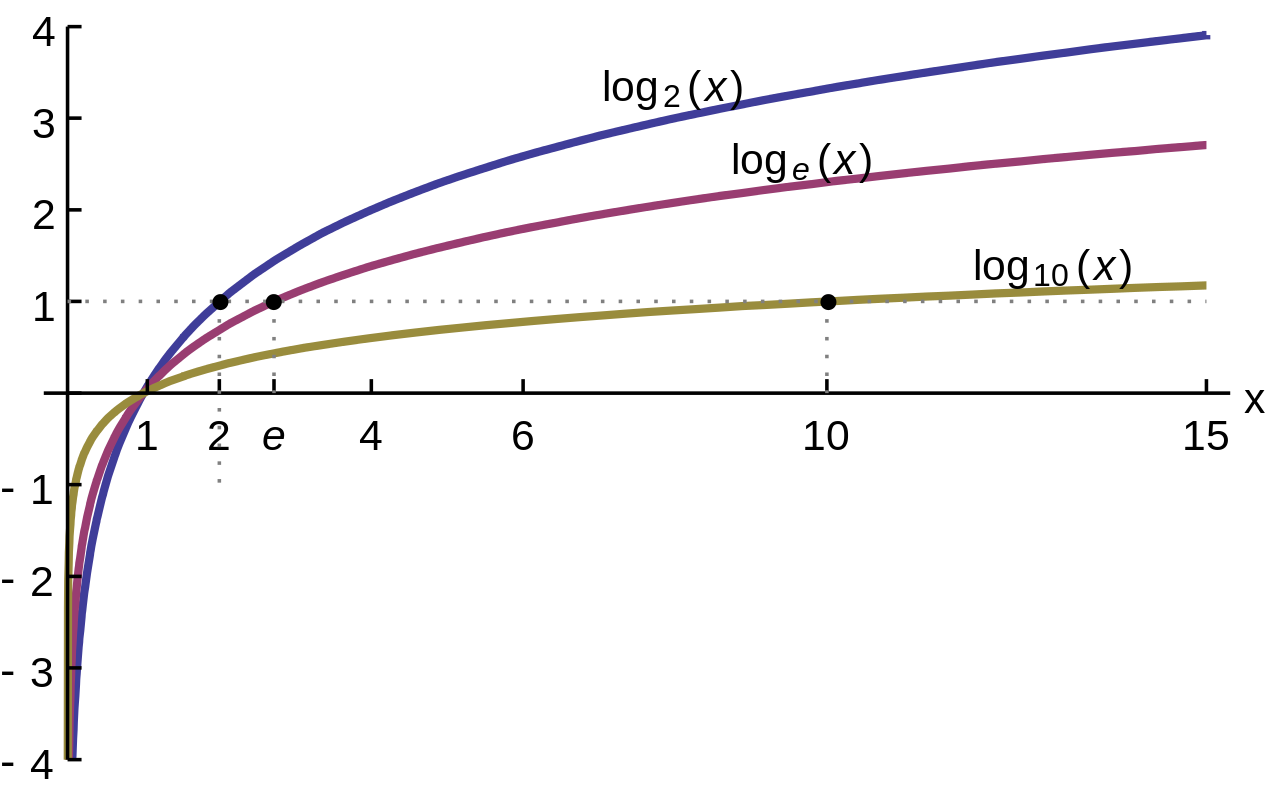
Đạo hàm của logarit là gì? Công thức đạo hàm của logaritĐạo hàm logarit là một công cụ quan trọng trong giải tích, đặc biệt hữu ích khi giải các bài toán có biểu thức phức tạp, hàm hợp, hàm mũ, hoặc khi cần đơn giản hóa quá trình tính đạo hàm. Dưới đây là những trường hợp cụ thể nên sử dụng đạo hàm logarit:
Khi hàm số có chứa logarit ngay từ đầu
Nếu hàm số cho sẵn ở dạng logarit như:
y=ln(x)
y=ln(u(x))
y=logₐ(x)
→ Khi đó, việc sử dụng đạo hàm logarit là trực tiếp và bắt buộc. Ta áp dụng công thức:
(d/dx)[ln(x)]=1/x
(d/dx)[ln(u)]=u' (x)/u(x)
(d/dx)[logₐ(x)]=1 / (x * ln(a))
Khi hàm số có dạng tích, thương, hoặc lũy thừa phức tạp
Trong các bài toán mà hàm số là tích hoặc thương giữa nhiều biểu thức, hoặc có lũy thừa, căn bậc, … việc đạo hàm trực tiếp sẽ rất rườm rà. Khi đó, logarit hóa là một phương pháp cực kỳ hiệu quả:
Ví dụ:
y=(x² + 1)^5 * sqrt(x + 3) / (x - 2)^3
→ Lấy logarit hai vế:
ln(y)=5ln(x² + 1)+(1/2)ln(x + 3) - 3ln(x - 2)
→ Sau đó đạo hàm hai vế để tính dy/dx
Phương pháp này gọi là lấy logarit hai vế và dùng đạo hàm logarit để đơn giản hóa biểu thức trước khi tính đạo hàm.
Khi nào nên sử dụng đạo hàm của logarit trong giải toán?Khi cần tính đạo hàm của hàm hợp có logarit
Với các hàm số như y=ln(u(x)) hoặc y=logₐ(u(x)), việc tính đạo hàm yêu cầu sử dụng quy tắc hàm hợp kết hợp với đạo hàm logarit:
d/dx[ln(u(x))]=u' (x)/u(x)
d/dx[logₐ(u(x))]=u' (x) / [u(x) * ln(a)]
Ví dụ:
Cho y=ln(3x + 1)
→ dy/dx=3 / (3x + 1)
Khi khảo sát hàm số hoặc tìm cực trị liên quan đến logarit
Trong các bài toán khảo sát hàm số, tìm cực đại – cực tiểu, đạo hàm được sử dụng để xác định các điểm dừng (f' (x)=0). Nếu hàm số có chứa logarit, ta phải đạo hàm chúng theo đúng công thức logarit đã học.
Ví dụ:
Khảo sát hàm: y=x * ln(x)
→ Đạo hàm: y' =ln(x)+1
→ Giải y' =0 để tìm cực trị
Khi giải bài toán thực tế có liên quan đến tăng trưởng, suy giảm, hoặc lãi suất
Trong các bài toán mô phỏng quá trình sinh học, tài chính, vật lý, … mà tốc độ thay đổi tỷ lệ thuận hoặc tỷ lệ nghịch với giá trị hiện tại, hàm logarit xuất hiện tự nhiên.
Ví dụ:
Bài toán lãi kép ngược → cần tìm thời gian gửi tiền: A=P * e^(rt) → dùng logarit để giải ẩn t
Bài toán phân rã phóng xạ, tăng trưởng vi khuẩn, hoặc độ pH trong hóa học
→ Tính đạo hàm để biết tốc độ thay đổi → cần dùng đạo hàm logarit
Khi cần rút gọn biểu thức đạo hàm trước khi tính giới hạn hoặc tích phân
Một số biểu thức khi đạo hàm bằng quy tắc logarit sẽ đơn giản hơn, dễ tính giới hạn hơn → giúp xử lý nhanh hơn trong các bài toán tích phân, giới hạn, khảo sát đồ thị.
✅ Tóm lại:
Sử dụng đạo hàm logarit khi:
Hàm số chứa logarit (ln, logₐ)
Hàm là tích, thương hoặc lũy thừa phức tạp → nên logarit hóa trước
Là hàm hợp có logarit → cần áp dụng quy tắc đạo hàm hàm hợp
Cần khảo sát, tìm cực trị, xét đơn điệu cho hàm chứa logarit
Trong bài toán thực tế về tăng trưởng, suy giảm, lãi suất, phân rã, …
Khi cần rút gọn biểu thức đạo hàm phức tạp để giải nhanh hơn

Làm sao để nhớ công thức đạo hàm của logarit nhanh và chính xác? Việc ghi nhớ công thức đạo hàm logarit không chỉ dựa vào học thuộc lòng, mà còn cần hiểu bản chất và áp dụng linh hoạt trong thực hành. Dưới đây là một số mẹo và phương pháp giúp bạn nhớ nhanh và chính xác:
✅ Nhớ công thức cơ bản nhất:
(d/dx) [ln(x)]=1 / x
→ Đây là công thức gốc, quan trọng nhất. Khi đã nhớ công thức này, các công thức khác có thể suy ra từ nó.
✅ Nhớ công thức đạo hàm hàm hợp:
Nếu y=ln(u(x)) ⇒ dy/dx=u' (x) / u(x)
Mẹo nhớ:
👉 " Đạo hàm tử – giữ mẫu"
Nghĩa là: lấy đạo hàm của bên trong (tử), giữ nguyên biểu thức bên trong (mẫu).
✅ Nhớ công thức log cơ số a:
(d/dx) [logₐ(x)]=1 / (x * ln(a))
Mẹo nhớ:
Cứ thấy logₐ(x) là chia thêm ln(a) ở mẫu.
Nếu a=e → trở về công thức cơ bản: ln(x)=logₑ(x) → không cần ln(a)
✅ Ghi nhớ bằng so sánh song song:
Biểu thức
Đạo hàm
ln(x)
1 / x
ln(u(x))
u' (x) / u(x)
logₐ(x)
1 / (x * ln(a))
logₐ(u(x))
u' (x) / (u(x) * ln(a))
✅ Luyện tập thường xuyên qua ví dụ đơn giản
Ví dụ 1:
y=ln(2x)
→ y' =2 / (2x)=1 / x
Ví dụ 2:
y=log₂(x³ + 1)
→ y' =[3x² ] / [(x³ + 1) * ln(2)]
→ Việc giải nhiều ví dụ sẽ giúp bạn quen tay, ghi nhớ tự nhiên mà không cần học vẹt.
✅ Liên hệ thực tế hoặc quy tắc “ so sánh”
Ví dụ:
Đạo hàm của mũ: (d/dx)[a^x]=a^x * ln(a)
→ Đạo hàm log: (d/dx)[logₐ(x)]=1 / (x * ln(a))
→ Mũ thì nhân ln(a), log thì chia ln(a)
✅ Tự viết lại công thức nhiều lần
Hãy viết lại công thức mỗi lần học → giúp tăng khả năng nhớ lâu thông qua hành động (muscle memory).
✅ Dùng flashcard hoặc app học công thức
Bạn có thể dùng giấy ghi chú nhỏ hoặc ứng dụng như Anki, Quizlet để tạo thẻ ghi nhớ công thức → học mỗi ngày 5 phút sẽ rất hiệu quả.

Các bài tập phổ biến liên quan đến đạo hàm của logarit trong đề thi? Tính đạo hàm của hàm số chứa logarit
✔️ Mục tiêu: Áp dụng trực tiếp công thức đạo hàm của ln(x) và logₐ(x)
✔️ Ví dụ đề thi:
Cho hàm số y=ln(3x - 1). Tính y' .
Đáp án: y' =3 / (3x - 1)
Đạo hàm hàm hợp có logarit
✔️ Mục tiêu: Áp dụng quy tắc đạo hàm hàm hợp
✔️ Ví dụ đề thi:
Cho y=log₂(x² + 1). Tính y' .
Giải: y' =(2x) / [(x² + 1) * ln(2)]
Sử dụng logarit để đạo hàm biểu thức phức tạp
✔️ Mục tiêu: Dùng phương pháp logarit hóa để rút gọn biểu thức trước khi lấy đạo hàm
✔️ Ví dụ đề thi:
Tính đạo hàm của y=[(x² + 1)^3 * sqrt(x + 2)] / (x³ - 1)^2
Hướng dẫn:
Lấy logarit hai vế:
ln(y)=3ln(x² + 1)+(1/2)ln(x + 2) - 2ln(x³ - 1)
Rồi đạo hàm từng vế để tìm dy/dx
Khảo sát hàm số có chứa logarit
✔️ Mục tiêu: Tính đạo hàm để xét tính đồng biến, nghịch biến, cực trị
✔️ Ví dụ đề thi:
Khảo sát sự biến thiên của hàm y=x * ln(x)
Tính đạo hàm: y' =ln(x)+1
Giải phương trình y' =0 để tìm cực trị
Lập bảng biến thiên

Bài tập Tìm hệ số thỏa mãn điều kiện đạo hàmTìm hệ số thỏa mãn điều kiện đạo hàm
✔️ Mục tiêu: Xác định tham số để hàm số có đạo hàm tại điểm hoặc có tính chất nào đó
✔️ Ví dụ đề thi:
Tìm a để hàm số y=ln(ax + 1) có đạo hàm tại x=1 bằng 2
→ Giải phương trình đạo hàm: a / (a + 1)=2
Bài toán thực tế có logarit
✔️ Mục tiêu: Giải bài toán có nội dung thực tế như tăng trưởng, phân rã, độ pH, lãi suất
✔️ Ví dụ đề thi:
Một chất phóng xạ phân rã theo công thức N(t)=N₀ * e^(-kt).
Tính tốc độ phân rã tại thời điểm t=5
→ Dùng đạo hàm N' (t)=-k * N₀ * e^(-kt)
So sánh tốc độ tăng trưởng của hai hàm logarit
✔️ Mục tiêu: Dùng đạo hàm để so sánh mức tăng của các hàm logarit
✔️ Ví dụ đề thi:
Cho f(x)=ln(x) và g(x)=log₃(x). So sánh f' (x) và g' (x) tại x=3
Tìm tiệm cận, giới hạn với logarit
✔️ Mục tiêu: Tính giới hạn bằng đạo hàm logarit
✔️ Ví dụ đề thi:
Tính lim x→ 0+của ln(1 + x) / x
Đáp án: 1
(Dựa vào định lý: lim x→ 0 ln(1 + x) / x=1)
✅ Gợi ý cách ôn tập hiệu quả:
Ôn lại công thức đạo hàm của hàm logarit cơ bản và hàm hợp
Tập trung vào kỹ năng biến đổi biểu thức bằng logarit hóa
Làm nhiều bài tập có tính ứng dụng thực tế và khảo sát hàm số
Luyện các đề thi năm trước để nhận diện dạng bài
Tóm lại, việc nắm vững công thức đạo hàm logarit không chỉ giúp bạn xử lý hiệu quả các bài toán trong chương trình phổ thông mà còn mở rộng khả năng ứng dụng vào các tình huống thực tế. Với cách ghi nhớ đúng, luyện tập đều đặn và hiểu rõ bản chất, bạn hoàn toàn có thể tự tin giải nhanh các bài toán liên quan đến logarit, đặc biệt trong các kỳ thi quan trọng. Hãy bắt đầu từ những công thức cơ bản và cùng rèn luyện thường xuyên để biến kiến thức thành kỹ năng vững chắc !