Công thức cấp số cộng cấp số nhân
✅ Cấp số cộng là gì?
Cấp số cộng là một dãy số mà mỗi số hạng (từ số thứ hai trở đi) bằng số hạng liền trước cộng với một số không đổi – gọi là công sai (d).
Công thức số hạng thứ n:
uₙ=u₁+(n - 1) * d
Ví dụ:
Dãy: 4, 7, 10, 13, 16, …
Ta có: công sai d=3 ⇒ là cấp số cộng.
✅ Cấp số nhân là gì?
Cấp số nhân là một dãy mà mỗi số hạng (từ số thứ hai trở đi) bằng số hạng liền trước nhân với một số không đổi – gọi là công bội (q).
Công thức số hạng thứ n:
vₙ=v₁ * q⁽ⁿ⁻¹ ⁾
Ví dụ:
Dãy: 3, 6, 12, 24, …
Ta có: công bội q=2 ⇒ là cấp số nhân.

Tổng quan về cấp số cộng và cấp số nhân📘 Cấp số cộng (CSC)
Số hạng thứ n:
uₙ=u₁+(n - 1) * d
Tổng n số hạng đầu:
Sₙ=(n / 2) * (u₁ + uₙ)
hoặc
Sₙ=(n / 2) * [2 * u₁+(n - 1) * d]
📘 Cấp số nhân (CSN)
Số hạng thứ n:
vₙ=v₁ * q⁽ⁿ⁻¹ ⁾
Tổng n số hạng đầu (với q ≠ 1):
Sₙ=v₁ * (qⁿ - 1) / (q - 1)
Tổng vô hạn (với 0 < |q| < 1):
S∞ =v₁ / (1 - q)
công thức cấp số cộng cấp số nhân
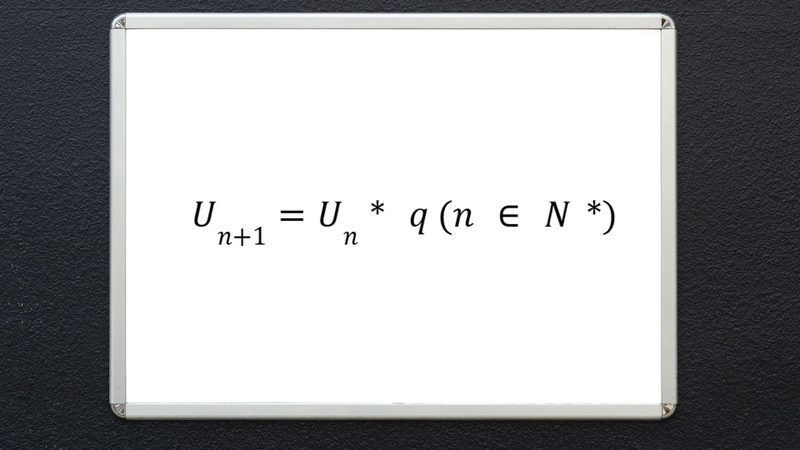
Công thức cần nhớ của cấp số cộng & cấp số nhân| Tiêu chí | Cấp số cộng (CSC) | Cấp số nhân (CSN) |
|---|
| Quy luật | Tăng/giảm đều (cộng d) | Tăng/giảm theo tỷ lệ (nhân q) |
| Hằng số đặc trưng | Công sai d | Công bội q |
| Số hạng tổng quát | uₙ = u₁ + (n - 1) * d | vₙ = v₁ * q⁽ⁿ⁻¹⁾ |
| Tổng n số hạng đầu | Sₙ = (n / 2) * (u₁ + uₙ) | Sₙ = v₁ * (qⁿ - 1) / (q - 1) |
| Có tổng vô hạn không? | ❌ Không có (tăng tuyến tính) | ✅ Có nếu `0 < |
| Ví dụ | 2, 4, 6, 8,… (d = 2) | 5, 10, 20, 40,… (q = 2) |
| Ứng dụng thực tế | Tăng lương định kỳ, chia đều tài nguyên,… | Tính lãi kép, nhân đôi vi khuẩn, giảm giá,… |
🧮 Cấp số cộng
Bài 1:
Cho u₁=2, d=5. Tìm u₁₀ và tổng 10 số hạng đầu.
Lời giải:
u₁₀=2+(10 - 1) * 5=47
S₁₀=(10 / 2) * (2 + 47)=5 * 49=245
Bài 2:
CSC có u₁=7, d=3. Tìm u₁₅ và S₁₅.
u₁₅=7+(15 - 1) * 3=7+42=49
S₁₅=(15 / 2) * (7 + 49)=7.5 * 56=420
Bài 3:
Cho dãy cấp số cộng: 5, 8, 11, 14, ...
a) Tìm công sai d và số hạng thứ 10 (u₁₀)
b) Tính tổng 10 số hạng đầu tiên (S₁₀)
Lời giải:
a)
u₁=5
d=8 - 5=3
u₁₀=u₁+(10 - 1) * d=5+9 * 3=5+27=32
b)
S₁₀=(10 / 2) * (u₁ + u₁₀)=5 * (5 + 32)=5 * 37=185
Bài 4:
Dãy cấp số cộng có u₁=7, d=-2. Tính tổng 15 số hạng đầu tiên.
Lời giải:
S₁₅=(15 / 2) * [2 * 7+(15 - 1) * (-2)]
S₁₅=(15 / 2) * [14+(-28)]=(15 / 2) * (-14)=-105
🧮 Cấp số nhân
Bài 1:
Cho v₁=2, q=3. Tìm v₅ và S₅.
v₅=2 * 3⁴=2 * 81=162
S₅=2 * (3⁵ - 1) / (3 - 1)=2 * (243 - 1)/2=242
Bài 2:
Dãy: 1, 2, 4, 8, … là cấp số nhân. Tính v₇ và tổng 7 số đầu.
v₇=1 * 2⁶=64
S₇=1 * (2⁷ - 1) / (2 - 1)=(128 - 1)=127
Bài 3:
Cho dãy cấp số nhân: 3, 6, 12, 24, ...
a) Tìm công bội q và số hạng thứ 6 (v₆)
b) Tính tổng 6 số hạng đầu tiên (S₆)
Lời giải:
a)
v₁=3
q=6 / 3=2
v₆=v₁ * q⁽⁶⁻¹ ⁾=3 * 2⁵=3 * 32=96
b)
S₆=3 * (2⁶ - 1) / (2 - 1)=3 * (64 - 1) / 1=3 * 63=189
Bài 4:
Dãy cấp số nhân có v₁=100, q=0.5. Tính tổng vô hạn của dãy.
Lời giải:
Vì |q|=0.5 < 1, có thể dùng công thức tổng vô hạn:
S∞ =v₁ / (1 - q)=100 / (1 - 0.5)=100 / 0.5=200
Bài tập mẫu có lời giảiỨng dụng của cấp số cộng (CSC)
- Cấp số cộng được ứng dụng nhiều trong các tình huống mà mức tăng hoặc giảm là đều đặn theo thời gian. Một số ứng dụng thực tế bao gồm:
- Tăng lương định kỳ: Trong doanh nghiệp, nhiều công ty áp dụng chính sách tăng lương theo mức cố định mỗi năm. Ví dụ, mỗi năm nhân viên được tăng 2 triệu đồng → tổng thu nhập qua nhiều năm tạo thành một cấp số cộng.
- Lãi suất đơn (simple interest): Trong trường hợp lãi suất không cộng dồn, tiền lãi mỗi kỳ là như nhau, tạo thành cấp số cộng.
- Chuyển động thẳng đều trong Vật lý: Nếu một vật chuyển động đều với vận tốc không đổi, quãng đường nó đi được sau mỗi khoảng thời gian bằng nhau sẽ tạo thành một cấp số cộng.
- Phân chia tài sản, chia phần thưởng: Khi cần chia đều một phần thưởng hay một khoản tài sản theo tỉ lệ tăng hoặc giảm đều, cấp số cộng được sử dụng để xác định số phần.
- Xếp ghế, xây bậc thang, thiết kế sân khấu: Số ghế trong mỗi hàng tăng đều, hoặc số bậc cầu thang cách đều – đây đều là những ví dụ ứng dụng trực tiếp cấp số cộng trong kiến trúc và xây dựng.
Ứng dụng của cấp số nhân (CSN)
Cấp số nhân thường xuất hiện trong các tình huống tăng trưởng hoặc giảm theo tỷ lệ phần trăm hoặc nhân với một hệ số nhất định. Ứng dụng thực tế rất phong phú, tiêu biểu có thể kể đến:
- Lãi kép (compound interest): Tiền gửi ngân hàng có lãi kép tăng theo cấp số nhân vì lãi của kỳ sau được tính trên cả gốc lẫn lãi kỳ trước.
- Tăng trưởng dân số: Khi dân số tăng theo tỷ lệ phần trăm cố định mỗi năm (ví dụ tăng 2% mỗi năm), số dân qua các năm sẽ tạo thành một cấp số nhân.
- Sự phân rã phóng xạ hoặc vi khuẩn phát triển: Số lượng hạt nhân phân rã hoặc vi khuẩn nhân đôi sau mỗi khoảng thời gian sẽ tạo thành một dãy cấp số nhân.
- Lan truyền thông tin, mạng xã hội, virus: Một nội dung lan truyền (viral) trên mạng xã hội theo cấp số nhân nếu mỗi người chia sẻ lại cho nhiều người khác.
- Giảm giá liên tiếp (giảm theo %) trong thương mại: Ví dụ: một món hàng giảm 10% mỗi tháng – sau nhiều tháng giá sản phẩm giảm theo cấp số nhân, chứ không phải cấp số cộng.
- Chi phí hoặc doanh thu tăng/giảm theo tỷ lệ: Trong kế hoạch tài chính, nếu doanh thu dự kiến tăng 15% mỗi quý, hoặc chi phí giảm 5% mỗi tháng, ta dùng cấp số nhân để tính toán.
🔚 Kết luận
Cấp số cộng và cấp số nhân là hai kiến thức nền tảng trong đại số, giúp giải quyết nhiều bài toán trong học tập lẫn thực tiễn. Việc nắm vững công thức cấp số cộng cấp số nhân số hạng tổng quát, công thức tính tổng, cùng với khả năng nhận dạng đúng loại dãy số sẽ giúp bạn học toán hiệu quả hơn và áp dụng tốt vào các tình huống thực tế như tính lãi, phân tích số liệu, dự đoán tăng trưởng, ... Đừng quên luyện tập công thức cấp số cộng cấp số nhân thường xuyên để thành thạo kỹ năng này !