Công thức cấp số cộng cấp số nhân
Cấp số cộng là gì?
Cấp số cộng (CSC) là một dãy số mà hiệu giữa hai số hạng liên tiếp luôn không đổi. Hiệu này được gọi là công sai, ký hiệu là d.
Công thức số hạng tổng quát:
uₙ=u₁+(n - 1) * d
Ví dụ:
Dãy số: 3, 6, 9, 12, 15, ...
Hiệu giữa các số liên tiếp là 3 → Đây là cấp số cộng với công sai d=3.
Cấp số nhân là gì?
Cấp số nhân (CSN) là một dãy số mà tỉ số giữa hai số hạng liên tiếp luôn không đổi. Tỉ số này được gọi là công bội, ký hiệu là q.
Công thức số hạng tổng quát:
vₙ=v₁ * q⁽ⁿ⁻¹ ⁾
Ví dụ:
Dãy số: 2, 4, 8, 16, 32, ...
Tỉ số giữa các số liên tiếp là 2 → Đây là cấp số nhân với công bội q=2.
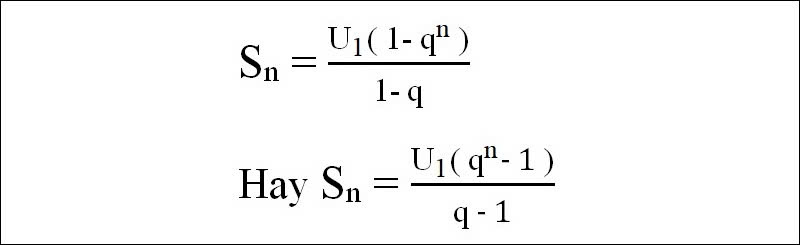
Cấp số cộng và cấp số nhân là gì?📌 Công thức cấp số cộng (CSC)
Số hạng tổng quát:
uₙ=u₁+(n - 1) * d
Trong đó:
uₙ là số hạng thứ n
u₁ là số hạng đầu tiên
d là công sai
n là số thứ tự của số hạng
Tổng n số hạng đầu tiên:
Sₙ=(n / 2) * (u₁ + uₙ)
hoặc
Sₙ=(n / 2) * [2 * u₁+(n - 1) * d]
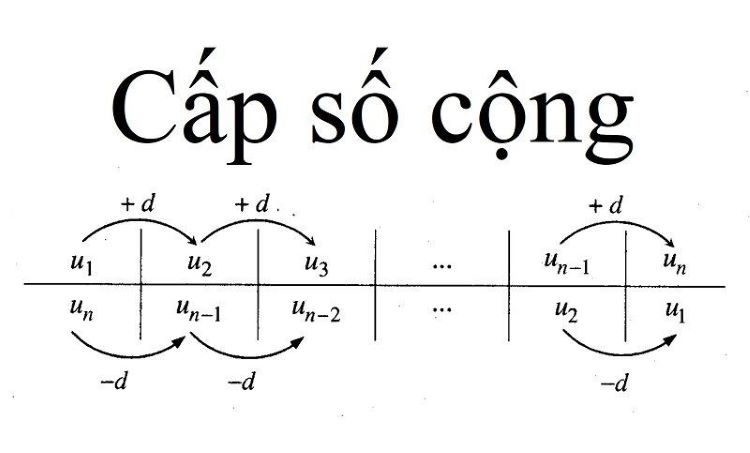
Công thức cấp số cộng📌 Công thức cấp số nhân (CSN)
Số hạng tổng quát:
vₙ=v₁ * q⁽ⁿ⁻¹ ⁾
Trong đó:
vₙ là số hạng thứ n
v₁ là số hạng đầu tiên
q là công bội
n là số thứ tự của số hạng
Tổng n số hạng đầu tiên (khi q ≠ 1):
Sₙ=v₁ * (qⁿ - 1) / (q - 1)
Tổng vô hạn (khi 0 < |q| < 1):
S∞ =v₁ / (1 - q)

So sánh cấp số cộng và cấp số nhân📊 So sánh cấp số cộng và cấp số nhân
| Tiêu chí | Cấp số cộng (CSC) | Cấp số nhân (CSN) |
|---|
| Quy luật | Hiệu giữa hai số liên tiếp không đổi | Tỉ số giữa hai số liên tiếp không đổi |
| Tên gọi hằng số | Công sai d | Công bội q |
| Công thức số hạng tổng quát | uₙ = u₁ + (n - 1) * d | vₙ = v₁ * q⁽ⁿ⁻¹⁾ |
| Công thức tính tổng n số hạng đầu | Sₙ = (n / 2) * (u₁ + uₙ) hoặc Sₙ = (n / 2) * [2 * u₁ + (n - 1) * d] | Sₙ = v₁ * (qⁿ - 1) / (q - 1) (với q ≠ 1) |
| Tổng vô hạn | Không có (vì tăng tuyến tính) | Có nếu `0 < |
| Ví dụ minh họa | 2, 4, 6, 8, 10,... (công sai d = 2) | 3, 6, 12, 24,... (công bội q = 2) |
| Tăng/giảm | Tăng hoặc giảm đều | Tăng hoặc giảm theo cấp số nhân |
| Ứng dụng | Lương tăng đều, khoảng cách, thời gian | Lãi kép, dân số, đầu tư tăng trưởng |
📘 Bài tập cấp số cộng (CSC)
Bài 1:
Cho cấp số cộng có số hạng đầu u₁=5, công sai d=3.
Tính số hạng thứ 10 và tổng 10 số hạng đầu.
Lời giải:
Số hạng thứ 10:
u₁₀=u₁+(10 - 1) * d=5+9 * 3=5+27=32
Tổng 10 số hạng đầu:
S₁₀=(10 / 2) * (u₁ + u₁₀)=5 * (5 + 32)=5 * 37=185
Bài 2:
Dãy số: 2, 6, 10, 14, ... là cấp số cộng.
Tìm số hạng thứ 15 và tổng 15 số hạng đầu.
Lời giải:
u₁=2, d=6 - 2=4
Số hạng thứ 15:
u₁₅=2+(15 - 1) * 4=2+56=58
Tổng 15 số hạng đầu:
S₁₅=(15 / 2) * (2 + 58)=7.5 * 60=450

Bài tập mẫu và lời giải về cấp số cộng cấp số nhân📘 Bài tập cấp số nhân (CSN)
Bài 3:
Cho cấp số nhân có số hạng đầu v₁=3, công bội q=2.
Tính số hạng thứ 6 và tổng 6 số hạng đầu.
Lời giải:
Số hạng thứ 6:
v₆=3 * 2⁵=3 * 32=96
Tổng 6 số hạng đầu:
S₆=3 * (2⁶ - 1) / (2 - 1)=3 * (64 - 1) / 1=3 * 63=189
Bài 4:
Dãy số: 5, 10, 20, 40, ... là cấp số nhân.
Tính số hạng thứ 8 và tổng 8 số hạng đầu.
Lời giải:
v₁=5, q=2
Số hạng thứ 8:
v₈=5 * 2⁷=5 * 128=640
Tổng 8 số hạng đầu:
S₈=5 * (2⁸ - 1) / (2 - 1)=5 * (256 - 1)=5 * 255=1275
Ứng dụng thực tế công thức cấp số cộng cấp số nhân
📌 Ứng dụng thực tế của cấp số cộng (CSC)
Tăng/giảm lương theo định kỳ
Khi mỗi năm một người được tăng lương cố định (ví dụ: 2 triệu/năm), thì tổng số tiền lương sau n năm là tổng của một cấp số cộng.
Công thức tổng:
Sₙ=(n / 2) * [2 * u₁+(n - 1) * d]
Chuyển động thẳng đều (vận tốc không đổi)
Quãng đường di chuyển sau mỗi đơn vị thời gian tăng đều → tạo thành một cấp số cộng.
Ví dụ: Ô tô đi được 10 km mỗi 1 giờ → quãng đường sau n giờ là CSC.
Sắp xếp ghế ngồi, phân phối vật phẩm
Khi số lượng vật tăng hoặc giảm đều theo từng bước, ta có thể dùng công thức CSC để tính tổng lượng cần thiết.
📌 Ứng dụng thực tế của cấp số nhân (CSN)
Tính lãi kép trong ngân hàng
Số tiền gửi ngân hàng với lãi suất cố định sẽ tăng theo cấp số nhân.
Công thức:
vₙ=v₁ * (1 + r)⁽ⁿ⁻¹ ⁾ (với r là lãi suất mỗi kỳ)
Tăng trưởng dân số hoặc tăng trưởng đầu tư
Nếu dân số tăng 2% mỗi năm, thì số dân mỗi năm sẽ tạo thành cấp số nhân.
Dự báo được dân số tương lai bằng công thức CSN.
Hiện tượng phân rã chất phóng xạ, vi khuẩn nhân đôi
Trong sinh học, nếu vi khuẩn nhân đôi mỗi giờ, tổng số lượng vi khuẩn sẽ tăng theo cấp số nhân.
Chiết khấu theo phần trăm liên tiếp
Khi giảm giá nhiều lần theo phần trăm (ví dụ: giảm 20% rồi lại giảm thêm 20%), giá trị còn lại không giảm đều mà theo CSN.
Bài viết trên đã cung cấp cái nhìn toàn diện về công thức cấp số cộng và cấp số nhân – hai khái niệm quan trọng trong toán học phổ thông. Bạn đã nắm được định nghĩa, công thức số hạng tổng quát, công thức tính tổng, cách phân biệt giữa hai loại cấp số cũng như các ví dụ minh họa dễ hiểu và ứng dụng thực tế trong cuộc sống như tính lãi kép, tính lương tăng theo năm, chuyển động đều, … Ngoài ra, các bài tập mẫu kèm lời giải giúp bạn vận dụng kiến thức một cách hiệu quả. Việc hiểu rõ và ghi nhớ các công thức này sẽ giúp bạn học tốt hơn, giải bài nhanh hơn và chuẩn bị vững vàng cho các kỳ thi. Hãy luyện tập thường xuyên để thành thạo và áp dụng linh hoạt vào thực tế.