 |
|
|
Thiết bị rửa mắt khẩn cấp
|
|
 |
|
|
|
|
|
 |
 |
|
|
Thiết bị an toàn ngành điện
|
|
 |
|
|
|
|
|
 |
|
 |
|
|
TIN TỨC
|
|
 |
|
|
Công thức đạo hàm logarit và cách hiểu dễ dàng cho người học
31 Tháng Bảy 2025 :: 11:43 CH :: 26 Views ::
0 Comments :: Blog
|
|
Tìm hiểu công thức đạo hàm logarit đơn giản, dễ hiểu. Hướng dẫn từng bước cách tính đạo hàm hàm log, ứng dụng vào bài tập và thực tế, phù hợp học sinh sinh viên. |
Công Thức Đạo Hàm LogaritLogarit là gì và xuất hiện ở đâu trong toán học?Logarit là một trong những hàm số quan trọng trong toán học, thường được viết dưới dạng log cơ số a của x. Nói đơn giản, logarit là cách bạn trả lời cho câu hỏi: “lũy thừa mấy thì được số đó?”. Chẳng hạn, log cơ số 10 của 1000 = 3, vì 10^3 = 1000. Logarit xuất hiện rất nhiều trong các bài toán về tăng trưởng, phân rã, âm học, điện tử, thống kê và đặc biệt là các bài toán hàm số trong chương trình lớp 12. Khi giải các bài toán liên quan đến cực trị, khảo sát hàm số, bạn cần biết cách tính đạo hàm của các hàm logarit để giải chính xác. Việc hiểu và nhớ công thức đạo hàm logarit không chỉ giúp bạn làm bài nhanh hơn mà còn tạo nền tảng cho việc học cao hơn ở đại học trong các môn liên quan đến vi phân và tích phân. 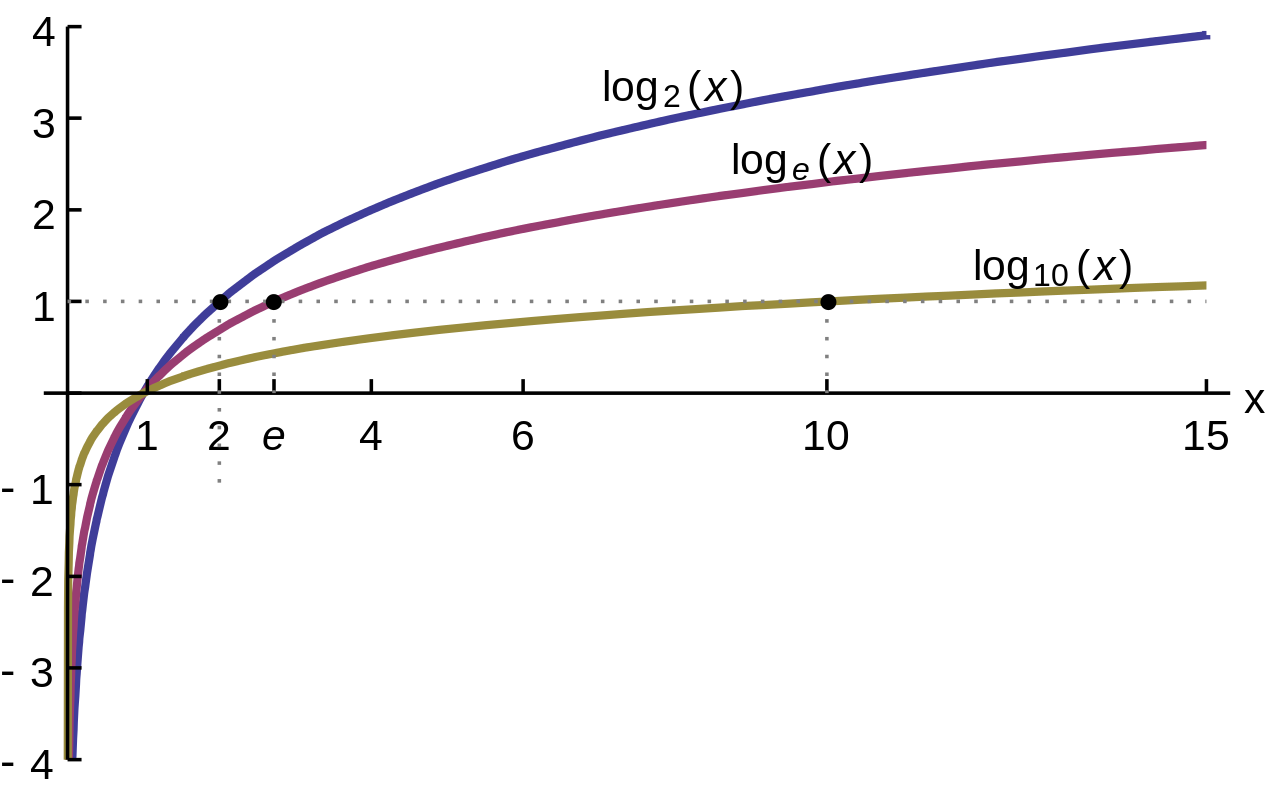
Đồ thị hàm số logarit cơ bảnĐạo hàm logarit cơ số e hay còn gọi là lnCông thức đạo hàm cơ bản đầu tiên cần nhớ là đạo hàm của hàm số ln(x), trong đó ln là viết tắt của logarit tự nhiên (logarit cơ số e), với e là một hằng số toán học đặc biệt, xấp xỉ 2.718. Công thức như sau: đạo hàm của ln(x) bằng 1 chia x Nói cách khác, nếu bạn có y bằng ln(x), thì y phẩy bằng 1 chia x. Đây là một trong những công thức cơ bản và quan trọng nhất trong đạo hàm hàm số logarit. Ví dụ, nếu y bằng ln(2x), thì đạo hàm của y là 1 chia 2x, sau đó nhân thêm đạo hàm của 2x là 2, kết quả cuối cùng là 1 chia x. Đạo hàm logarit cơ số a bất kỳ Nếu bạn có hàm số y bằng log cơ số a của x, trong đó a là một hằng số dương khác 1, thì công thức đạo hàm là 1 chia x nhân với 1 chia ln(a). Điều đó có nghĩa là, bạn cần tính thêm logarit tự nhiên của cơ số a để hoàn tất công thức. Ví dụ, đạo hàm của log cơ số 2 của x sẽ là 1 chia x nhân với 1 chia ln(2). Bạn có thể dùng máy tính để tính ln(2) nếu cần kết quả số. 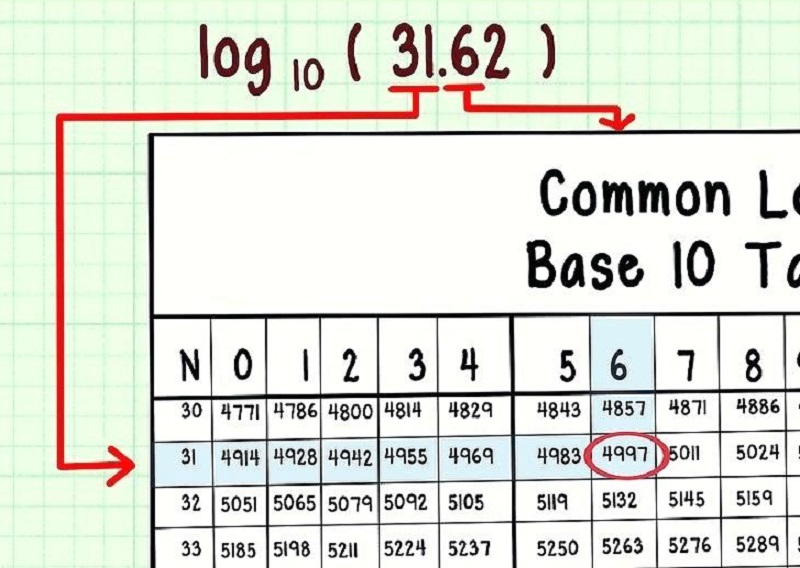
Công thức đạo hàm logarit cơ bản và mở rộngKhi logarit không phải của x đơn thuầnTrong nhiều bài toán, hàm logarit không đơn giản là log của x, mà là log của một biểu thức phức tạp hơn, chẳng hạn log của căn bậc hai của x cộng 1, hoặc log của một hàm chứa ẩn. Khi đó, bạn cần áp dụng quy tắc đạo hàm hàm hợp. Nghĩa là, bạn lấy đạo hàm của log bình thường như trên, sau đó nhân thêm đạo hàm của biểu thức bên trong dấu log. Chẳng hạn, nếu y bằng ln(x bình phương cộng 1), thì đạo hàm của y sẽ là 1 chia x bình phương cộng 1, sau đó nhân với đạo hàm của x bình phương cộng 1 là 2x. Kết quả cuối cùng là 2x chia cho x bình phương cộng 1. Khi logarit là hàm phức kết hợp với nhân chiaTrong một số bài toán nâng cao, logarit xuất hiện dưới dạng nhân hoặc chia giữa các biểu thức chứa x. Khi đó, bạn có thể áp dụng các quy tắc biến đổi logarit để tách thành tổng hoặc hiệu của nhiều hàm đơn giản. Ví dụ, ln(x nhân với x cộng 2) có thể tách thành ln(x) cộng ln(x cộng 2). Sau đó, bạn lấy đạo hàm từng phần, áp dụng công thức cơ bản và cộng lại. Việc biến đổi như vậy giúp bạn dễ xử lý hơn, đặc biệt là trong bài toán khảo sát hàm số, giải phương trình hoặc tìm cực trị. 
Cách đạo hàm logarit của hàm hợp và biến đổi tíchPhân tích biểu thức và chọn công thức phù hợpBí quyết để giải đúng các bài toán đạo hàm logarit là xác định đúng dạng hàm trước khi áp dụng công thức. Nếu hàm là log cơ số e, bạn áp dụng công thức đơn giản nhất. Nếu hàm là log cơ số khác, bạn thêm hệ số 1 chia ln(a). Nếu hàm là log của biểu thức, bạn dùng đạo hàm hàm hợp. Trước khi tính, hãy đơn giản biểu thức nếu có thể bằng các công thức logarit cơ bản như log nhân biến thành tổng, log chia biến thành hiệu, log lũy thừa biến thành hệ số nhân. Điều này giúp rút gọn phép tính và tránh sai sót. Sau khi áp dụng đạo hàm, đừng quên rút gọn biểu thức kết quả nếu có thể để đảm bảo đáp án gọn gàng và dễ so sánh với đáp án trắc nghiệm nếu là bài thi Luyện tập thường xuyên với nhiều dạng bàiĐạo hàm logarit tuy không quá khó nhưng rất dễ sai nếu bạn quên công thức hoặc bỏ qua đạo hàm phần bên trong. Hãy luyện tập nhiều dạng khác nhau, từ hàm cơ bản đến hàm hợp, kết hợp với phân tích đề bài kỹ càng để làm quen và tăng tốc khi làm bài thi. Bạn có thể bắt đầu với các ví dụ đơn giản như đạo hàm của ln(x), log cơ số 2 của x, sau đó nâng cấp lên các dạng phức tạp như log của căn x, log của x mũ 3, hoặc logarit nhân với hàm đa thức. Mỗi dạng bài đều có cách tiếp cận riêng nhưng đều xuất phát từ công thức cơ bản bạn đã học. Từ bài tập lớp học đến công nghệ và kinh tếĐạo hàm logarit không chỉ dùng để giải bài tập trong chương trình phổ thông mà còn xuất hiện trong rất nhiều lĩnh vực khác. Trong kinh tế, đạo hàm log giúp xác định tốc độ tăng trưởng theo tỷ lệ phần trăm. Trong hóa học, logarit được dùng để tính pH, và đạo hàm giúp mô tả sự biến đổi nồng độ. Trong kỹ thuật và vật lý, đạo hàm log xuất hiện trong các mô hình sóng, dòng điện, áp suất và âm thanh.
Công thức đạo hàm logarit là một trong những nội dung quan trọng và có tính ứng dụng cao trong học tập cũng như thực tiễn. Khi hiểu rõ bản chất logarit, biết cách phân tích biểu thức và áp dụng đúng công thức, bạn có thể giải quyết mọi dạng bài từ cơ bản đến nâng cao. Hãy luyện tập đều đặn và đừng ngại đặt câu hỏi khi gặp khó khăn, vì càng hiểu sâu, bạn sẽ càng thấy toán học thú vị và hữu ích.
|
|
|
 |
|
|
| Comments |
Hiện tại không có lời bình nào!
|
|
Gửi lời bình
Huỷ Bỏ
|
|
|
|
 |
|
|